Quantum Mechanics Simulation

For today’s recreational coding exercise, we will look at quantum mechanical systems, in particular, the Schrodinger-Poisson equations. We will create a simulation for the evolution of a wavefunction under its self-potential. Such a system may describe certain superfluids/Bose-Einstein condensate or exotic dark matter.

Before diving in, below is a gif of simulation looks like:

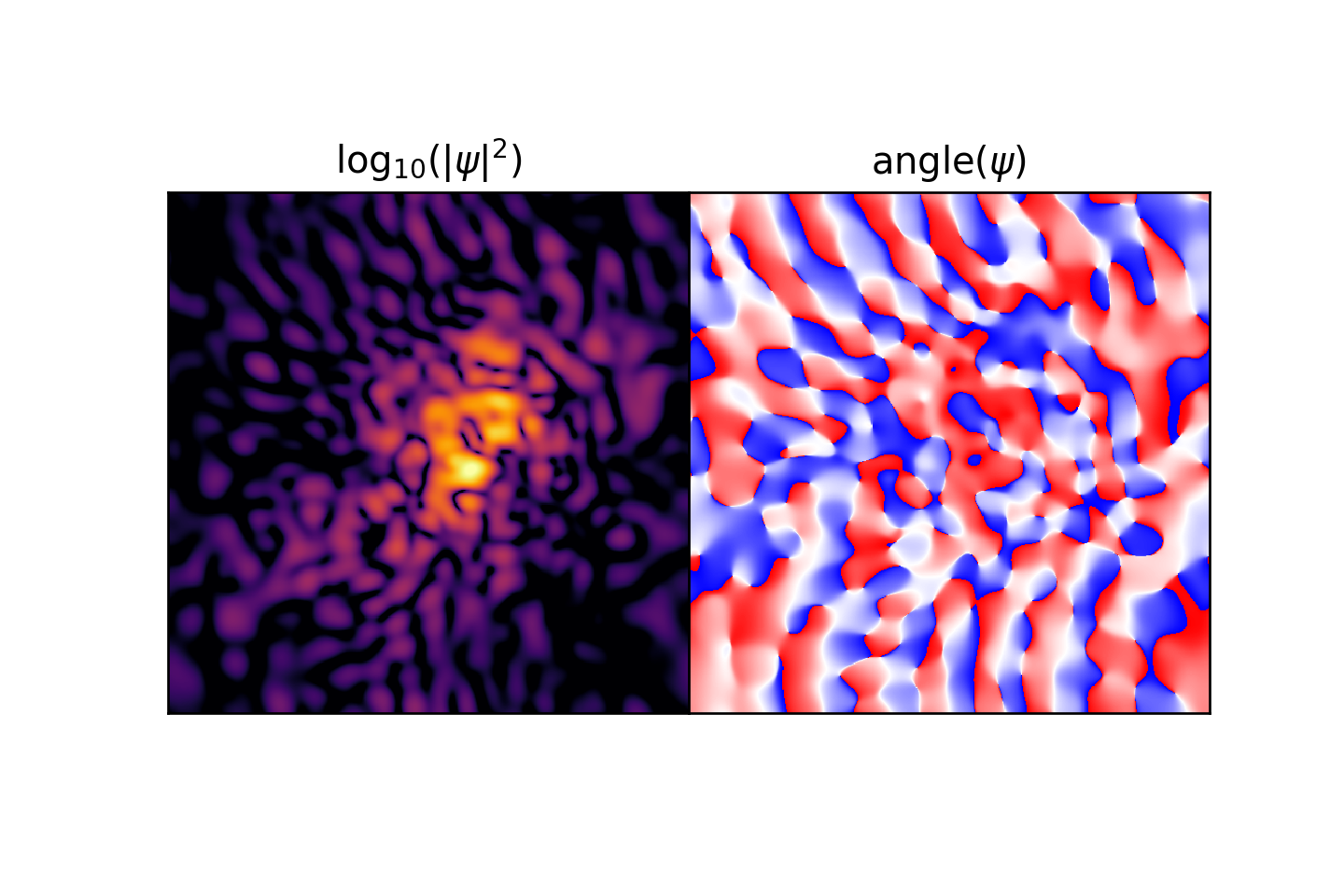
Schrodinger-Poisson Equations

We will consider the evolution of the wavefunction ψ(x) under the Schrodinger equation:

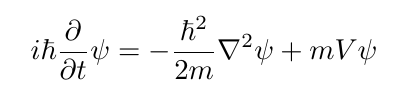
The wavefunction ψ describes the quantum field in the domain with spatial coordinate x. It is normalized such that its spatial average is unity:

In the equation, m is the particle mass and h-bar (ℏ) is the reduced Planck’s constant.The wavefunction feels the effect of the potential V, which in our example we assume it is the self-potential given by Poisson’s equation:

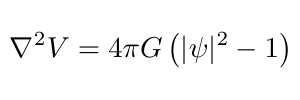
where G is Newton’s gravitational constant. Such a system of equations is relevant to the study of quantum wave dark matter, also known as fuzzy dark matter. It is easy to implement all sorts of other potentials to study different quantum systems. For example, implementing a static potential such as the Coulomb potential models the Hydrogen atom. Another example would be the quantum harmonic oscillator.

In the discussion that follows, we will keep notation simple by assuming a system of units with:

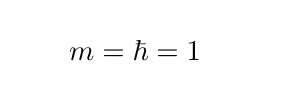
Spectral Method

A spectral method uses the Fast Fourier Transform (FFT) algorithm to transform the solution on thephysical domain x into a superposition of waves each described by a wavenumber k. This method turns out to be especially useful for evolving the Schrodinger equation as well as for solving the Poisson equation. The details of the FFT is beyond the scope of our exercise today, but the algorithm is a common tool and has efficient implementations in many programming languages and we offer a high-level discussion of how and why it is useful.

The FFT transforms the wavefunction:

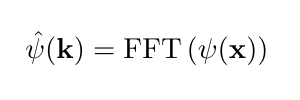
Applying a Fourier transform to the Schrodinger equation will thus replace:

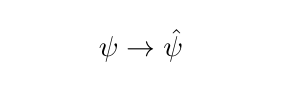
In addition it will change gradients ∇ as:

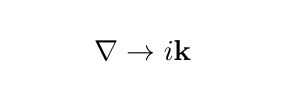
which is part of the reason why the method is so powerful. In Fourier space, taking the derivative becomes just simple multiplication by a vector. It is easy to multiple numbers.The Laplacian operator in the Schrodinger equation will thus transform as:

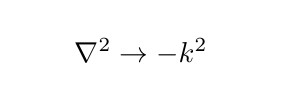
Ignoring the potential term in the Schrodinger equation for a second, and applying the Fourier transform, we have the equation:

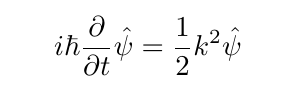
If we discretize time into stepsΔt, then, the Fourier transform of the wavefuntion can be updated from one timestep to the next with what is called a drift operator: